Como interpretar figuras tridimensionais nos vestibulares?

Geometria do Espaço é um daqueles temas que sempre são cobrados tanto nos vestibulares como no Enem e, portanto, dominá-lo, e também ter algumas estratégias na hora de encarar questões desse assunto, pode fazer uma grande diferença em seu desempenho.

Nesse contexto, uma pergunta que sempre é feita pelos alunos é a seguinte: é possível criar métodos para reconhecer propriedades de figuras tridimensionais?

A resposta é um grande SIM! Com algumas dicas e um pouco de organização, você pode acertar muitas questões envolvendo Geometria do Espaço.

Vamos a elas:

I. A primeira dica é algo que vale para todas as disciplinas. Fique antenado com o que está acontecendo no mundo. Um grande exemplo foram as Olimpíadas no Rio; a quantidade de situações em que a Geometria Espacial surge naturalmente é enorme, desde o cálculo do volume de uma bola de basquete, passando pela quantidade de água em uma piscina, até a representação do movimento do giro de um atleta no lançamento de disco.

II. Sempre que possível faça uma boa figura para representar o problema. Em muitos exercícios reconhecer triângulos em um corte em um sólido, permite aplicar relações de semelhança ou o teorema de Pitágoras e, a partir daí, responder às perguntas feitas.

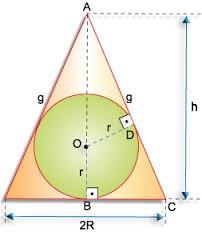
Representação de uma secção meridiana de um cone e uma esfera inscrita nesse cone. Os triângulos retângulos ADO e ABC são semelhantes.

III. Cuidado com pequenas confusões! Fique ligado: quando você lê prisma, não desenhe uma pirâmide! (o mesmo vale para cilindro e cone).

IV. Em exercícios que cobram a descrição de movimentos no espaço tridimensional e suas representações em um plano, procure se colocar na situação de observador, posicionando o objeto entre você e o plano. Por exemplo, em uma gangorra se buscamos a projeção do movimento no solo, imagine-se olhando de cima. Caso a projeção seja em um muro, “coloque-se” de modo a ter a gangorra entre você e o muro.

V. Em provas de múltipla escolha, cuidado com as alternativas! Frequentemente, as bancas examinadoras colocam alternativas erradas em que algum equívoco previsível foi cometido. Pode ser desde uma falha de cálculo, uma interpretação errada no texto ou uma projeção diferente da que foi pedida.

Com essas dicas e um pouco de treino, conhecendo a teoria, você certamente conseguirá acertar muitos exercícios nos vestibulares e no Enem.

Agora é com vocês, bom trabalho e sucesso!

Antonio Carlos Russo é graduado em matemática Pura e Mestre em Sistemas Dinâmicos pela USP.